前言
写在前面的话:数据结构与算法。
对于初识数据结构的小伙伴们,鉴于后面的数据结构的构建会使用到同tag前面的内容,包括具体数据结构的应用,所使用到的数据结构,也是自己构建的,未使用系统的库文件,因此,建议这类小伙伴们按顺序进行学习;
对于想查询有关资料的小伙伴们,可以选择性地浏览。希望大家都能有所收获~
上一章我们了解了图的一些基本概念,
本章我们来介绍图的两种最重要的搜索算法:广度优先搜索算法和深度优先搜索算法。
广度优先搜索算法
广度优先搜索(也叫宽度优先搜索,缩写BFS)是连通图的一种遍历算法,这一算法也是很多重要的图的算法的原型。下几章将要介绍的Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和广度优先搜索类似的思想。这是一种盲目搜索法,它并不考虑结果的可能位置,而是彻底地搜索整张图,直到找到结果为止。一般用队列结构来辅助实现BFS算法。
广度优先搜索的核心思想:对于某个节点,BFS总是先遍历该节点的所有邻接节点。
下面我们用一系列图示来理解BFS的遍历过程:
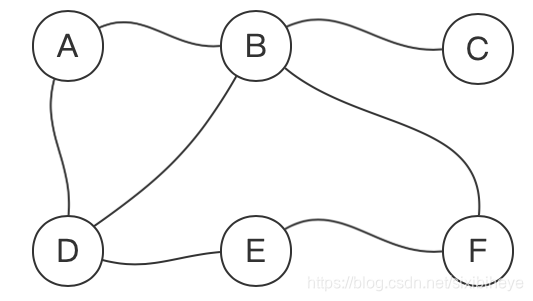
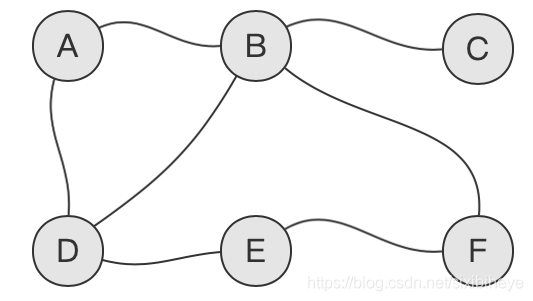
上图中,我们从节点A出发,进行BFS搜索,首先,遍历A节点(标灰):
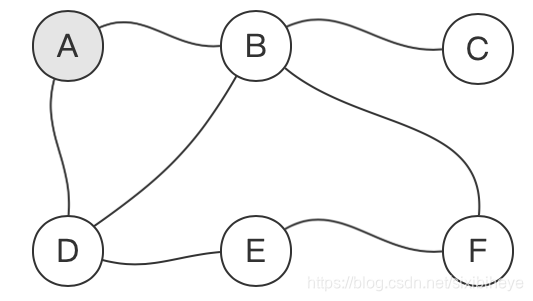
然后,遍历A节点的所有邻接节点----B和D:
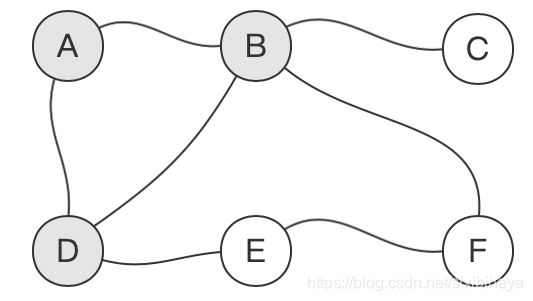
对于已遍历的B和D,遍历B的所有邻接节点C(注意,对于B的已访问的邻接节点A,D,不会再次进行访问),遍历D的所有邻接节点E(对于D的已访问的邻接节点A,B,不会再次进行访问)(此外先遍历B或D均可):
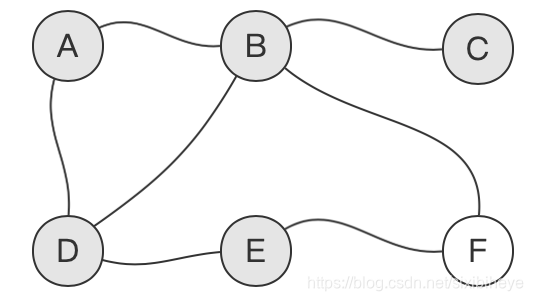
继续同上,遍历C,E的所有邻接节点 ,由于C的所有邻接节点均已访问,故节点C的遍历结束。E还有未被访问的邻接节点F,故遍历F:
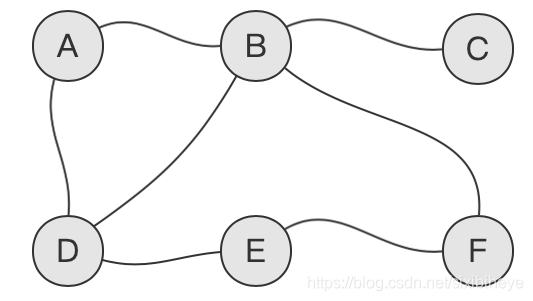
此时节点F的所有邻接节点均已被访问,故节点F的遍历结束。
之后,全图搜索是否还有未被访问的节点,如何有,选取任意一个未被访问的节点,重复上述遍历,直至所有的节点均被访问,BFS结束。
此时,该图的一种BFS搜索的结果序列为:A-->B-->D-->C-->E-->F。
从上述的过程可以看出,BFS搜索的结果序列是不唯一的,读者可以想一想下面的序列是不是BFS搜索得到的?
- A–>D–>B–>C–>E–>F
- A–>B–>D–>C–>E–>F
- A–>B–>D–>E–>F–>C
(答案在文末)
深度优先搜索算法
深度优先搜索(DFS,Depth First Search)是针对图的一种遍历算法。利用深度优先搜索算法可以产生对应图的拓扑排序表,利用其拓扑排序表可以方便地解决很多相关的图问题。一般用栈结构来辅助实现DFS算法。
深度优先搜索的核心思想:对某一条路径,DFS会一直深入到不能深入为止,接着回溯至上一节点继续搜索。
同样的,我们已一系列图示来理解DFS的搜索过程:
用上面同样的图:
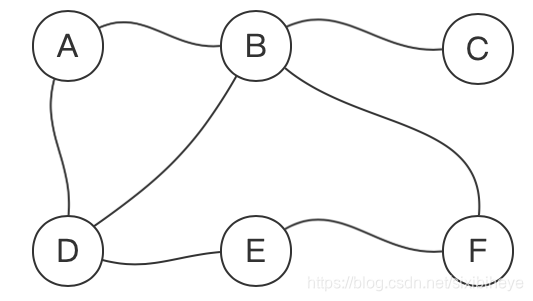
随机取一个节点,比如节点A,访问它,将其标灰:
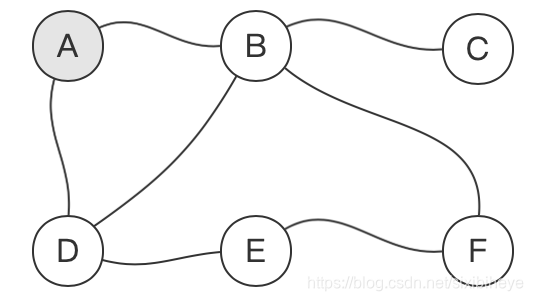
然后,从节点A开始,沿某一条路径一直深入(顺次访问路上的每个节点)直至不能深入为止,如A-->B-->D-->E-->F,注意遍历至F后不会再遍历B,同一节点只能访问一次:
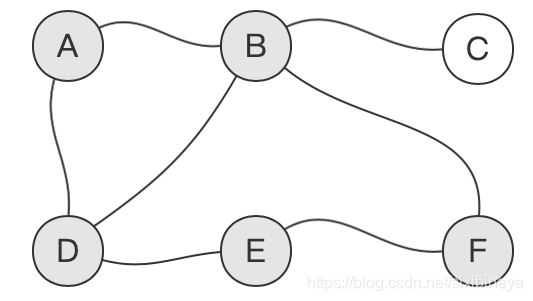
此时,DFS已搜索至节点F,由于节点F已经没有未被访问的分支来继续深入,这时,DFS搜索会“**回溯”**到节点F的上一个节点-----E,如果节点E还有未被访问的分支,继续访问并深入直至不能深入为止;如果节点E的分支均已被访问,则继续“**回溯”**到节点E的上一个分支,重复以上操作。这样,一直回溯到节点B的时候,发现节点B有一个未被访问的分支:B-->C,因此访问并深入这条路径:
重复上述过程(深入+回溯),当回溯到起始路径(A-->B-->D-->E-->F)的起始节点A时,节点A没有未被访问的分支,从而这条路径搜索完毕。
接着,全局搜索是否还有未被访问的节点,如果有,任意取一个未被访问的节点,继续上述过程,直至回溯到该节点…;如果没有,则全图搜索完毕。
我们得到了DFS的搜索结果序列:A-->B-->D-->E-->F-->C。
同BFS一样,DFS搜索的结果序列是不唯一的。请读者思考下面的序列是不是DFS的搜索结果?
- A–>B–>D–>C–>E–>F
- A–>D–>B–>C–>F–>E
- A–>D–>E–>F–>B–>C
最后,请读者细细体会BFS和DFS的原理,尤其是DFS中关于回溯的过程,这是算法领域里一种非常重要的思想。这两种搜索方式不仅适用于图,也适用于树等具有关联特性的结构。掌握这两种搜索方式,是学习图中其他内容的基础。
最后,附上文前答案:(BFS搜索结果:1,2;DFS搜索结果:3,5,6)
下一章,我们将介绍图中另外一个重要的概念-----拓扑排序。

